The new era of spatial systems in topography and geodesy

2007/02/01 Bastarrika Izagirre, Aitor - Kartografia eta Geodesia ingeniaria eta Topografia Ingeniaritza Teknikoko irakasleaEHU | Elgezabal Otsoa De Txintxetru, Aitziber - EHUko Topografia Ingeniaritzako irakaslea | Artano Perez, Karmele - EHUko Topografia Ingeniaritzako irakaslea Iturria: Elhuyar aldizkaria

• Telekomunikazioak
• Teknologia
• Geografia

The topography aims to represent the natural and artificial characteristics of the Earth. It therefore analyzes the methods and techniques necessary to measure, receive and publish graphic and spatial information of any point or element of the Earth.

In order to locate and represent the elements of the Earth, topography must know the shape and dimensions of the Earth, which is what geodesy science offers.

Changes in recent decades

The first advances in topography and geodesy took place after World War II. Then they developed a lot of electronics, mechanics, optics, mathematics, physics... that revolutionized the geomatic sciences, including topography and geodesy, developing new methods and tools. These methods perform electronic measurement of distance and angles from electromagnetic waves. Subsequently, the development of computer science allowed the development of software for the management of both mathematical and geographical data, allowing the automatic realization of complex manual calculations.

The next revolution has come from the hand of the satellites. Since the 1970s, the use of artificial satellites has brought enormous benefits to topography and, above all, geodesy. In fact, in addition to precisely locating points far apart from each other, spatial geodesia has opened up new possibilities to study the shape of the Earth, the geodynamics of the Earth and the force of gravity. Without a doubt, we can affirm that methodologically we are facing a revolution: having overcome the classics of geodesy and topography, the GNSS (Global Navigation Systems) space systems have opened new paths, both in conventional topographic works and in geodesy works and research.

Location

Understanding how the user's location is determined by spatial systems is relatively simple. Location coordinates (X,Y and Z) are calculated by the trilateration method.

Trilateration is a common method in topography. With this method, measuring the distance between a point such as point A and three fixed points with known coordinates, the position coordinates of point A (X, Y and Z) can be obtained.

In space systems, the known points are satellites, and the position of the receiver is known by measuring the distance from where the receiver is located to satellites. The satellites continuously emit radio signals and, to calculate the distance, the time elapsed from the satellite to the receiver is measured and multiplied by the speed of light. It is said that this is a passive system, since the receptors only receive signals. Through this system, millions of people can know their location simultaneously.

To measure time, satellites have high-precision atomic clocks. Atomic clocks are able to accurately measure time. The clocks of the receivers, on the other hand, are less precise, but they reach a great precision, since it is estimated mathematically the difference between the clocks of the satellites and the clocks of the receivers. For this estimate to be possible it is necessary to know the minimum distance of a receiver to four satellites. Mathematically, three unpublished location coordinates (X, Y and Z) would suffice, but the fourth satellite allows solving the fourth unknown, i.e. the receiver clock error.

Pseudodistance and measurements by phase

To measure the distance from the receiver to the satellites there are two methodologies: code measurement and phase measurement.

In addition to the signal, the satellite sends a modulated code to a certain wave frequency. By correlation of this code you can know the time it takes the signal to reach the receiver, and multiplying this data by the speed of light you get to know the distance between the satellite and the receiver. This distance measurement is called pseudodistance. Navigation receivers indicate this, for example, the receivers used in both vehicles and mountains. This method achieves an accuracy in the location of 15-30 meters.

However, the accuracy of 15-30 meters is clearly unacceptable for geodesy and topography, where accuracy of a few millimeters and centimeters is required. Therefore, in these cases, the distances from the satellite to the receiver are measured by the wave phase. Phase measurements are based on the wave itself and not on the codes modulated therein. And since the wavelength of the wave is a few centimeters, the distance can be measured much more accurately and an exact location can be obtained. However, phase measurement presents a major obstacle. Although the signal that reaches the receiver can easily be known the wave gap, it is not so easy to know the total number of cycles. It is the problem of cycle ambiguity. To understand it there is a XIX. A good example of the 20th century.

XIX United States. The eighteenth century Great Plain meters measured the public land that crossed the open fields as follows: in a cart full of stones or stakes three people went; one led the car; the other, with a compass, kept the car in the direction to follow; and the last, counted the number of turns that had given a piece of cloth attached to the cart. When the cloth circled as much as a mile, they put a stone or a stake and went on.

The satellite positioning system is equivalent to the person measuring the number of revolutions of the wheel, with the difference that when you climb the car you lie behind and sleep. When you wake up you will worry and start trying to figure out the distance; you know that at that time the wheel is in the middle of the tour, but you don't know how many complete turns you have given. This is the case of cycle ambiguity: the receiver knows the gap, but not the number of complete cycles.

The total number of cycles is calculated using software, algorithms, which in recent years have improved considerably: in a short time (in a few seconds or in a few minutes) they can know the number of cycles. For calculating the total number of cycles, these algorithms must contain at least instantaneous data from another receiver. Therefore, with a single receptor you can know only pseudo-distance.

Phased differential localization

In topography and geodesy, phased differential location is used for high-precision measurements. This methodology allows to know with great precision the three-dimensional vector (called baseline) between two receptors. The calculation of this vector necessarily requires simultaneous data of two topographic-geodesic receptors.

The differential location is based on the fact that the signals reaching both receivers suffer the same errors. Since the satellites are about 20,000 kilometers away, the signals emitted by them have to make a long journey through the ionosphere and the troposphere to reach the receiver, in which they suffer a series of changes or errors.

It can be assumed that this journey is the same for the two receivers, so the satellite signal will have the same error on the two receivers, allowing to obtain the vector between receivers with enormous precision (precision in millimeters to ten kilometers). From there, and being one of the two receptors placed at a point of known coordinates (fixed exactly on a tripod, on the point), the position of the second receptor is calculated: knowing the exact coordinates of the origin of the vector, it is possible to know precisely the coordinates of the second point of the vector.

This method allows the calculation of the location after the observations, both in the office and at the time. The current location is called RTK (Real Time Kinematic). In the works performed by RTK, the receiver located in known coordinates (called base) sends real-time data obtained from the satellite to the other receiver (called mobile), usually by radio signals. As this radio signal has a limited range, you can not move too far the mobile from the base, up to 30 kilometers if there are no obstacles between them. However, in recent years the data collected in the database is also sent via GPRS taking advantage of extended mobile phone networks.

GPS, GLONASS and Galileo

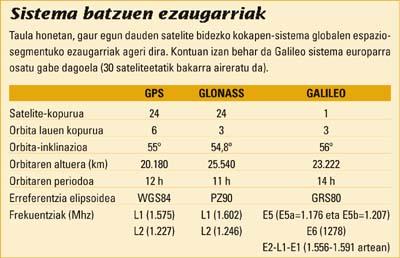
Currently there are two satellite positioning systems available: GPS and GLONASS. A third, Galileo, begins to build.

The first was GPS, created by the U.S. Department of Defense for military purposes. The NAVSTAR constellation is the GPS system. The GLONASS system, for its part, was created by the Soviet Defense Service and subsequently ceded to the Russian Space Agency. They, in addition to giving military use, reinforced civil use, but very late, so today it is used less than GPS. However, by relying on military services, none of them ensures a permanent signal.

Galileo will be the European satellite navigation system. This system will offer great accuracy and, depending on civil control, will permanently guarantee a global positioning service. Galileo is an initiative of the European Union and the European Space Agency. It is a constellation of 30 satellites: the first satellite (and the only one at the moment) was launched on 28 December 2005.

Today more and more receivers can receive the signal from both the GPS and the GLONASS system. Some receivers used in topography and geodesy, for example, allow both systems to be used, increasing the number of satellites and improving accuracy.

The constellation of Galileo will also contribute to this. On the one hand, under the same conditions, the satellites of the constellation of Galileo will calculate their location more accurately than the other two systems, having more precise atomic clocks. And on the other hand, compatibility with GPS and GLONASS systems will allow greater precision when more satellites are available: when more signals are received, the results of the adjustments will be more accurate and will allow results in places where no signals are currently received or where the number of satellites is not enough to calculate the location.

Advantages and future of space systems

The global positioning and navigation satellite system offers great advantages in geodesy and topography.

The classical methods used so far have allowed to achieve the position of a point, so it is necessary to guarantee the visibility between a known point and the one that was wanted to be located. On the other hand, global satellite positioning systems allow obtaining a position between unvisible points, as base lines of tens or hundreds of kilometers can be achieved with precision in centimeters. In addition, unlike so far, global satellite positioning systems allow measurements in any climate situation.

In the field of topography, when carrying out the surveys, fertility has increased considerably in the work carried out by the satellite system. In conventional topography two people are needed to perform the work, while with satellite positioning systems only one person can work and also earn points per day.

They also have limitations. The most important thing is to work in places that hinder the signal of satellites: higher obstacles, buildings and trees, such as destroying the signal of satellites and, in many cases, it is impossible to get its location. Looking ahead, however, when the Galileo system is available, the increase in satellites will allow to exceed this limit in several places.