Tangram

1989/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Xa trouxemos os puzzles ou “cabezudos” e algúns xogos chineses, as damas e o xadrez. Nesta ocasión traémosche a un “crebacabezas” chinés: O famoso TANGRAM. E dicímolo famoso, seguramente porque xa o coñeces. (Figura 1).

Figura .

Empecemos lembrando a súa historia.

XIX. Na introdución dun libro sobre os crebacabezas chineses do século XX pódese ler que a orixe do tangram (e mesmo o inventor) era descoñecido.

O nome chinés do Tangram é Ch’i Ch'ae pan (xogo dos sete elementos). Chu alto (740-330 a.C.) A palabra é. O nome provén dun costume chinés. E é que o sétimo día do sétimo mes era feliz pasar un fío polo sete zuelos dunha agulla.

Os primeiros libros publicados sobre o tangram aparecen na época do emperador Ch’ing Chia Ch’ing (1796-1820), o primeiro en 1813. Con todo, o xogo xa estaba moi estendido. En Europa, por exemplo, parece que o primeiro libro apareceu en 1805.

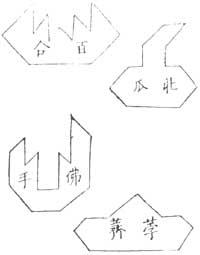
Os libros chineses divídense en dous partes. Na primeira exponse problemas e na segunda exponse solucións. Os problemas levan un símbolo chinés coa intención de explicar o significado da imaxe, aínda que esta é tan cadrada como abstracta (ver figura 2).

Figura .

O xogo suporía un gran éxito, tal e como indica a chea de libros publicados desde 1813. Estendeuse rapidamente por Europa e América e paira 1818 xa se podían atopar libros en Alemaña, Gran Bretaña, Francia, Italia e Austria. En 1817 M. Publicouse un artigo de Williams no que se presentan una serie de exercicios matemáticos que poden resolverse con axuda do tangram. O propio Napoleón, durante o seu exilio, foi un gran amante do tangram.

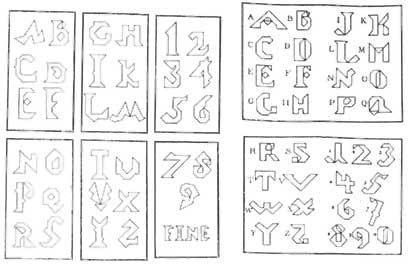
Os libros europeos e americanos eran principalmente copias de chineses. Con todo, achegaron ao tangram, a letra e cifra máis árabe. Aínda que dixemos una achega, fixéronse diferentes versións destas letras e cifras (ver figura 3).

Se nun principio uno dos atractivos do xogo era poder crear novas imaxes, aos poucos esa vantaxe foise perdendo (pero aínda non acabou do todo).

Tangram non é un xogo de competición, senón individual.

O xogo está formado por sete pezas lisas, como dous triángulos pequenos (iguais), un triángulo, un cadrado e un romboide (cada un pode estar formado por dous triángulos pequenos anteriores) e dous triángulos grandes (que poden estar formados por catro triángulos pequenos) (ver figura 1). Este xogo non ten regras. Con todo, ten dous límites ou regras:

1. Todas as imaxes deben completarse con sete pezas.
2. Todas as imaxes son launas (non se poden facer pirámides).

Alfabeto e cifras de Der Kopfzerbrecher.Figura .

Respectando estas dúas condicións, o xogador poderá facer o que desexe coas fichas (por exemplo, o romboide pode ser utilizado por ambas as caras).

Figura .

Convexas Tangram

Coas pezas do Tangram pódense formar infinitas imaxes. Basta con mover un pouco una peza nunha imaxe. Pero demos un pouco de seriedade ou rigor ao xogo.

Como se pode apreciar, todas as pezas do xogo son convexas. A pregunta agora é: Cantas imaxes convexas pódense construír co tangram? Esta vez a resposta non é infinita, non. En 1942 Fu Traing Wang e Chuan Chih Hsiung demostraron que estas imaxes convexas terán un máximo de oito lados. Logo, tendo en conta que as imaxes convexas enmárcanse dentro dun rectángulo, tamén se demostrou que se creaban 20 imaxes convexas.

Só 13 delas pódense construír con pezas do tangram (ver figura 5). Nestas probas supuxeron que estas imaxes convexas debían construírse utilizando 16 triángulos como os pequenos triángulos, xa que o tangram pódese dividir en 16 triángulos pequenos.

Figura .

Tangram divisibles

Con este nome, se se dividen as pezas do tangram en dous grupos, trátase de nomear os que se obteñen formando as mesmas figuras coas pezas de cada grupo (ver figura 6).

Figura .

Paira terminar diremos que non faltan outros xogos “tangram” que se parecen ao tangram chinés. A continuación móstrase este ovo e algunhas imaxes que se poden completar coas súas pezas. (Ver figura 7).

Aínda que poderiamos dicir máis cousas, creemos que o mellor paira entender ben o tangram é xogar. Aquí tes una pequena mostra das posibilidades que ofrece o xogo. (Ver figura 8). Téntao!