Txirrindularien banaketa

Txirrindularien itzuliak direla eta, askotan aprobetxatzen dugu aukera hori lagun arteko apostuak egiteko.

Partaide bakoitzari txirrindulari batzuk asignatzen zaizkio aleatorioki eta hauek egiten dutenaren arabera irabazten edo galtzen du partaideak.

Hona ondoren apostu posible bat:

Etapako irabazlea duenari, bakoitzak duro bana emango dio. Egunero egiten da apostu hau.

• Itzuliko irabazlea duenari (bukatzen denean) bakoitzak 50 pta. emango dizkio. Bigarrena duenari, bakoitzak 25 pta., eta hirugarrena duenari, 10 pta.

Tarteko helmugetako irabazlea duenari, bakoitzak 10 pta. emango dizkio (itzuli osoa bukatzen denean).

Mendi-portuetako irabazlea duenari, bakoitzak 25 pta. emango dizkio (itzuli osoa bukatzen denean).

Ekipo-sailkapeneko irabazlea duenari, bakoitzak 25 pta. emango dizkio (itzuli osoa bukatzen denean).

Honako hau, txirrindulariak zozketatzen lagunduko dizun programa da.

Oharrak:

1.- Aurreko alean aleatorioen errepikaketa-arazoa aztertu genuen. Oraingo honetan zera egin behar dugu: zenbaki-multzo bat (txirrindulariei dagokiona) aleatorioki ordenatu. Beraz, bi baldintza izan behar ditugu kontutan:

Amaierako zerrendan zenbaki bakoitzak behin bakarrik azaldu behar du.
Zerrenda horretan zenbaki guztiek egon behar dute.
Problema hau ebazteko, ondoko urratsak emango ditugu:
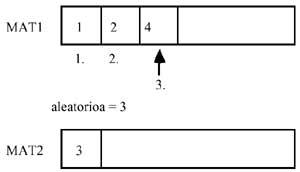
Aleatorioki ordenatu behar den zerrenda taula batean gorde (MAT1) (360 lerroa)
Zenbaki aleatorioa ateratzen denean, taula honen indize bezala erabiliko da eta aleatorioak adierazten duen lekuan dagoen elementua beste taula batera (MAT2) pasako da (390-410 lerroak)
Ondoren zenbaki berbera berriro atera ez dadin, elementu hori matrizetik kendu egin beharko da, atzekoak posizio bat aurreratuz.
Honetaz gain, aleatorioen eremua ere eguneratu egin beharko da, elementu bat borratzen den bakoitzean bat gutxiagotuz (420-440 lerroak).
Ohar zaitez aleatorioa errepikatzen bada ere, aleatorio horrek adierazten duen posizioan jadanik lehen zegoen zenbakia ez dela egongo. Honela amaierako zerrendan zenbakiak errepikatuta egotea ebitatuko da.
Bestalde, prozesu hau lehenengo taula edo matrizeko elementu guztiak borratu arte errepikatzen denez, hasierako elementu guztiak egongo dira bigarren zerrendan.

2.- Banaketa ahalik eta berdinena egin asmoz, taldetako buruak beste taula batean sartu dira, lehenengo hauek banatuz (110-120 lerroak). Gerta daiteke partaide guztientzat txirrindulari-kopuru berdina ez tokatzea ere. Kasu hauetan partaide desberdinen artean diferentziarik handiena batekoa izan dadin idatzi da programa (210-270 lerroak).

3.- Txirrindulari gutxiagorekin gelditu behar duten partaideak beti berak izan ez daitezen, partaideak ere aleatorioki ordenatzea iruditu zaigu irtenbiderik egokiena (90-100 lerroak).

4.- Programa honetan ez ditugu txirrindularien izenak kontutan hartu; daramatzaten zenbakiak baizik.

5.- Programa egikaritu aurretik sar itzazu 1010 lerroan zozketan parte hartu behar duzuen guztien izenak.

6.- Guk ezarritako mugak hauek dira:
Txirrindulari-kopurua: 200
Ekipo-kopurua: 20
Partaide-kopurua: 20
Muga hauek gainditu nahi izanez gero, nahikoa izango da 20 lerroan matrizeen dimentsioak aldatzea.

10 REM TXIRRINDULARIAK
20 DIM TXIRRIN1(20),TXIRRIN2(200),PARTAIDE(20),
MAT1(200),MAT2(200)
30 KEY OFF : SCREEN 2,0 : CLS
40 LOCATE 3,28:PRINT "TXIRRINDULARIEN BANAKETA":
LOCATE 4,28:PRINT "========================"
50 LOCATE 10,10: INPUT "Zenbat txirrindulari dira guztira";KOP1
60 LOCATE 12,10: INPUT "Zenbat ekipo dira";EKI
70 LOCATE 14,10: INPUT "Zenbat lagunek hartu behar
duzue parte zozketan";KOP2
80 K=0 : KK=0
90 KOP=KOP2 : GOSUB 330 : REM ORDENATU EGIKARITU
100 FOR II=1 TO KOP2 : PARTAIDE(II)=MAT2(II)+1 : NEXT II
110 KOP=EKI : GOSUB 330 : REM ORDENATU EGIKARITU
120 FOR II=1 TO EKI : TXIRRIN1(II)=MAT2(II)*10+1 : NEXT II
130 KOP=KOP1 : GOSUB 330 : REM ORDENATU EGIKARITU
140 FOR II=1 TO KOP1
150 IF (MAT2(II)+1) MOD 10 1 THEN TXIRRIN2(JJ)=
MAT2(II)+1 : JJ=JJ+1
160 NEXT II
170 CLS
180 BURU=INT(EKI/KOP2) : SOBRA=EKI-(KOP2*BURU) :
BESTEAK=INT((KOP1-EKI)/KOP2)
: MINI=INT (KOP1/KOP2) : SOBRA1=KOP1-(MINI*KOP2)
190 FOR II=1 TO KOP2
200 RESTORE 520
210 FOR JJ=1 TO PARTAIDE(II) : READ PART$ : NEXT JJ
220 PRINT : PRINT PART$
230 IF II = SOBRA THEN BURU1=BURU+1 ELSE BURU1=BURU
240 IF II = SOBRA1 THEN MINI1=MINI+1 ELSE MINI1=MINI
250 HARTU = MINI1-BURU1
260 FOR JJ=1 TO BURU1 : K=K+1 : PRINT TXIRRIN1(K); : NEXT JJ
270 FOR JJ=1 TO HARTU : KK=KK+1 : PRINT
TXIRRIN2(KK); : NEXT JJ
280 NEXT II
290 END
300 REM AMAIA TXIRRINDULARIAK
310 REM
320 REM
330 REM ORDENATU EKINTZA
340 J=0
350 RANDOMIZE TIMER
360 FOR II=1 TO KOP : MAT1(II)=II-1 : NEXT II : II=KOP
370 REM BITARTEAN
380 IF II=0 THEN 460
390 C = INT (RND * KOP) + 1
400 J = J + 1
410 MAT2(J) = MAT1(C)
420 FOR JJ=C TO KOP-1 : MAT1(JJ) = MAT1(JJ+1) : NEXT JJ
430 II = II - 1
440 KOP = KOP - 1
450 GOTO 370
460 REM AMBITARTEAN
470 RETURN
480 REM AMAIA ORDENATU EKINTZA
490 REM
500 REM
510 REM PARTAIDEEN IZENAK
520 DATA "1.PARTAIDEA","2.PARTAIDEA","3.PARTAIDEA",
"4.PARTAIDEA","5.PARTAIDEA","6.PARTAIDEA","7.PARTAIDEA",
"8.PARTAIDEA","9.PARTAIDEA","10.PARTAIDEA"
530 REM AMAIA PARTAIDEEN IZENAK