Casting cycliste

1988/04/01 Arrojeria, Eustakio - Elhuyar Zientziaren Komunikazioa | Lizaso, Pili - Informatika SailaElhuyar Fundazioa Iturria: Elhuyar aldizkaria

• Programazioa

En raison des tours des cyclistes, nous profitons souvent de cette occasion pour parier entre amis.

Chaque participant est randomisé par plusieurs cyclistes, gagnant ou perdant en fonction de ce qu'ils font.

Voici un pari possible:

Au vainqueur de l'étape, chacun vous livrera un dur. Ce pari est placé quotidiennement.
• Personne gagnante du remboursement (une fois terminé) 50 ptas. chacune. il les livrera. Le second, 25 ptas. chacun et le troisième, 10 ptas.

Au vainqueur des destinations intermédiaires, chacun 10 ptas. livraison (une fois le tour complet terminé).

Au gagnant des ports de montagne, chacun 25 ptas. livraison (une fois le tour complet terminé).

Au vainqueur du classement des équipes, chacune 25 m. livraison (une fois le tour complet terminé).

C'est un programme qui vous aidera à contourner les cyclistes.

Observations:

1.- Dans le numéro précédent, nous analysons le problème de répétition des aléatoires. A cette occasion, nous devons randomiser un ensemble de nombres (correspondant aux cyclistes). Il faut donc tenir compte de deux conditions:

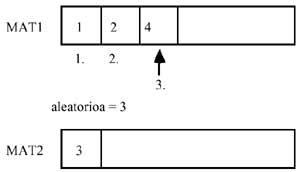
Dans la liste finale chaque numéro ne doit apparaître qu'une seule fois. Cette liste doit contenir tous les numéros. Pour résoudre ce problème, nous allons suivre les étapes suivantes: Une fois le nombre aléatoire extrait, il sera utilisé comme index de ce tableau et l'élément situé à l'endroit indiqué par l'aléatoire passera à une autre table (lignes 390-410). Pour éviter de répéter le même nombre, cet élément doit être retiré de la matrice, avant une position ultérieure. En outre, la zone aléatoire doit être mise à jour en réduisant un élément à chaque effacement (lignes 420-440). Notez que même si l'aléatoire est répété, le nombre qui existait déjà n'existera pas dans la position qui représente cet aléatoire. De cette façon, les numéros ne seront pas répétés dans la liste finale. D'autre part, puisque ce processus est répété jusqu'à ce que tous les éléments de la première table ou matrice soient effacés, tous les éléments initiaux seront dans la deuxième liste.

2.- Afin de rendre la distribution aussi équitable que possible, les chefs des groupes ont été inclus dans une autre table, en séparant les premiers (lignes 110 à 120). Il peut arriver que tous les participants n'aient pas le même nombre de cyclistes. Dans ces cas, le programme a été élaboré afin que la plus grande différence entre les participants soit d'un seul participant (lignes 210-270).

3.- Pour que les participants qui doivent rester avec moins de cyclistes ne soient pas toujours les mêmes, la meilleure solution a été d'ordonner au hasard les participants (lignes 90-100).

4.- Dans ce programme, nous n'avons pas pris en compte les noms des cyclistes, mais les numéros qu'ils portent.

5.- Entrez dans la ligne 1010 tous les noms que vous allez participer au tirage avant d'exécuter le programme.

6.- Nos limites sont: Nombre de cyclistes : 200 Nombre d'équipes : 20 Participants: 20 Pour dépasser ces limites, il suffit de modifier les dimensions des matrices sur la ligne 20.

10 CYCLISTES REM 20 DIM TXIRRIN1(20),TXIRRIN2(200),PARTICIPANT(20), MAT1(200),MAT2(200) 30 KEY OFF : SCREEN 2,0 : CLS 40 LOCATE 3,28:PRINT "CASTING: cyclistes" LOCATE 4,28:PRINT "================================ 50 EMPLACEMENT 10,10: INPUT "Nombre total de cyclistes";KOP1 60 LOCATE 12,10: INPUT "Combien d'ordinateurs sont";EKI 70 LOCATE 14,10: NUM.1(Nombre de participants)