Repartición ciclista

1988/04/01 Arrojeria, Eustakio - Elhuyar Zientziaren Komunikazioa | Lizaso, Pili - Informatika SailaElhuyar Fundazioa Iturria: Elhuyar aldizkaria

• Programazioa

Debido ás voltas dos ciclistas, moitas veces aproveitamos esta ocasión paira apostar entre amigos.

A cada participante asígnanselle aleatoriamente varios ciclistas, gañando ou perdendo en función do que fagan.

A continuación una posible aposta:

Ao gañador da etapa, cada un entregaralle un duro. Esta aposta realízase diariamente.
• Persoa gañadora da devolución (una vez finalizada) 50 ptas. cada una. entregaraos. O segundo, 25 ptas. cada un e o terceiro, 10 ptas.

Ao gañador dos destinos intermedios, cada un 10 ptas. entrega (una vez finalizada a volta completa).

Ao gañador de portos de montaña, cada un 25 ptas. entrega (una vez finalizada a volta completa).

Ao gañador da clasificación de equipos, cada un 25 pts. entrega (una vez finalizada a volta completa).

Este é un programa que che axudará a sortear ciclistas.

Observacións:

1.- No número anterior analizamos o problema de repetición de aleatorios. Nesta ocasión, debemos ordenar aleatoriamente un conxunto de números (correspondente aos ciclistas). Por tanto, hai que ter en conta dúas condicións:

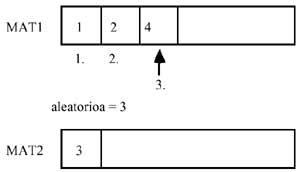
Na lista final cada número só debe aparecer una vez. Esta lista debe conter todos os números. Paira resolver este problema imos seguir os seguintes pasos: Una vez extraído o número aleatorio, utilizarase como índice desta táboa e o elemento situado no lugar indicado polo aleatorio pasará a outra táboa (liñas 390-410). Paira evitar que se repita o mesmo número, este elemento deberá eliminarse da matriz, adiantando una posición posterior. Ademais, deberase actualizar a área de aleatorios reducindo un cada vez que se borre un elemento (liñas 420-440). Advírtase que aínda que se repita o aleatorio, na posición que representa este aleatorio non existirá o número que xa existía. Desta maneira evitarase que os números estean repetidos na lista final. Por outra banda, dado que este proceso repítese ata que se borren todos os elementos da primeira táboa ou matriz, todos os elementos iniciais estarán na segunda lista.

2.- Co fin de facer a distribución o máis equitativa posible, os xefes dos grupos incluíronse noutra táboa, separando os primeiros (liñas 110 a 120). Pode ocorrer que non todos os participantes teñan o mesmo número de ciclistas. Nestes casos redactouse o programa para que a maior diferenza entre os participantes sexa dun só participante (liñas 210-270).

3.- Para que os participantes que teñen que quedar con menos ciclistas non sexan sempre os mesmos, a mellor solución foi ordenar aleatoriamente aos participantes (liñas 90-100).

4.- Neste programa non tivemos en conta os nomes dos ciclistas, senón os números que levan.

5.- Introduce na liña 1010 todos os nomes dos que ides participar no sorteo antes de executar o programa.

6.- As nosas limitacións son: Nº de ciclistas: 200 Número de equipos: 20 Asistentes: 20 Si deséxase superar estes límites bastará con modificar as dimensións das matrices na liña 20.

10 CICLISTAS REM 20 DIM TXIRRIN1(20),TXIRRIN2(200),PARTICIPANTE(20), MAT1(200),MAT2(200) 30 KEY OFF : SCREEN 2,0 : CLS 40 LOCATE 3,28:PRINT "REPARTICIÓN DE CICLISTAS": LOCATE 4,28:PRINT "==========================" 50 LOCATE 10,10: INPUT "Número total de ciclistas";KOP1 60 LOCATE 12,10: INPUT "Cantos equipos son";EKI 70 LOCATE 14,10: NUM.1(Nº DE PARTICIPANTES)