Número oro

1992/09/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

“... dos cosas no se pueden combinar sin tercero, es necesario un vínculo que los une, y no hay mejor que uno mismo y lo que reúne, todo igual y único. Y la naturaleza de la proporción alcanza ese objetivo, ya que de tres números, o de tres masas, o de cualquiera de las tres fuerzas, la proporción con respecto al último es la misma que con respecto al último, y, por otra parte, cuando la proporción con respecto al último es la misma que con el primero de ellos (el intermedio se convierte en el primero y el último en el medio), todos permanecen intencionadamente igual que antes, formando parte de una relación similar”.

Platón, “Conversaciones, Timeo”

El origen del número de oro es antiguo. No se puede saber desde cuándo el hombre conoce (apika, harean pentagrama, makila sin levantar, que podía imaginar desde que era consciente). Los egipcios ya lo conocían, pero fue Euclides quien lo definió:

“Un derecho está dividido en la proporción entre las cabezas y la bisectriz cuando la proporción entre la mayor y la mayor es la misma entre ésta y la menor”.

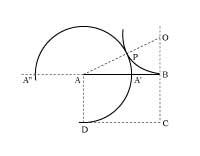
Por ejemplo, en la figura 1, la parte AA' es el segmento oro o sección del segmento AB,

AA' = A'BAB = AA'

Se cumple la proporción.

Si el lector no cree que compruebe una regla. Independientemente del segmento AB,

AA'

=

A'B

? AB = AA' = ?

el cociente que da la sección de oro toma siempre el mismo valor:

d = 0,618033988

Es un número algebraico irracional d cuya expresión concreta es:

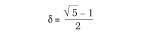
Este número nos sorprende en la Antigüedad, en el Renacimiento y en la actualidad.

Mencionaremos dos propiedades curiosas:

Si a d le añadimos 1 o le damos la vuelta, obtendremos el mismo valor:

1 + ? = 1 / ? edo1 + 0,618033... Restando = 1,618033 = 1 / 0,618033...1-i ? o calculando ?2, obtendremos el mismo valor:1 – ? = ?2 edo1 – 0,618033... = 0,391966... = (0,618033...)2

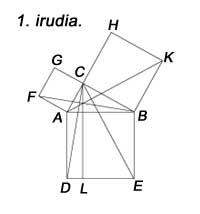
Desde la antigüedad se conocen los métodos de división de un segmento en proporción áurea (1. irud. ). La proporción de oro se encuentra también en muchas figuras geométricas.

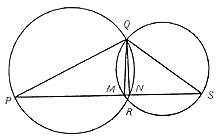
El más conocido es el pentagrama (o estrella de cinco vértices), símbolo mágico de los pitagóricos y alquimistas (2. irud. ). A pesar de que en el Renacimiento se dio una gran importancia a la proporción de oro, tanto en teoría como en la práctica, no se utilizó por primera vez en el Renacimiento. Por el contrario, en la pirámide de Keops (3. irud. ), Se utilizó ya en el Partenón de Atenas, Catedral de Chartres, etc.

Figura . Pentagrama o estrella de cinco vértices inscrita en el pentágono. La principal y a la vez más mágica de las figuras doradas. En sus dimensiones relativas se basa el número de oro:

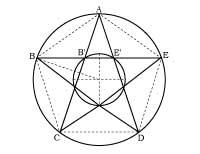
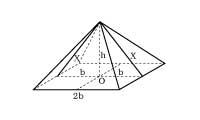
Figura . Según el geógrafo griego Herodoto, que describió las pirámides egipcias, la altura h de la pirámide de Keops es la mitad de la base b y la mitad del apotema x. Es decir,

Esto significa que la sección áurea de b x y, por tanto, el perímetro de la base es igual a la longitud de la circunferencia de altura h. Por esta razón hay quien cree que algunos egipcios conocían el cuadro del círculo. No es necesario recurrir a los atlánticos o marcianos. El secreto de la gran pirámide radica en sus dimensiones de oro:\ ª 4> ? aprox.

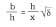
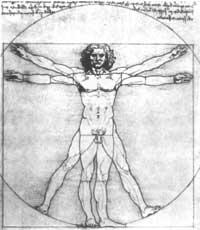
También se encuentra en el propio cuerpo humano. Según el “canon” de Leonardo, las proporciones más bellas y armoniosas del cuerpo se obtienen cuando están en proporción dorada. Leonardo metió al “hombre brillante” en un círculo cuyo centro es el mismo y cuyo radio está en una proporción dorada con la altura del hombre (4. irud. ).

Los científicos del Renacimiento adecuaban al número de oro el valor de la ley universal de la armonía. No se equivocaban, XVII. Según demostró Kepler en el siglo XX. Las proporciones de oro aparecen en las distancias entre planetas. El número de oro indica cuándo un año concreto corresponde a un ciclo lunar de 19 años.

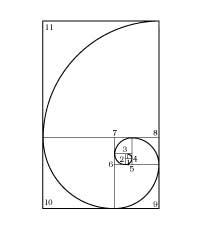
La sección áurea también se encuentra en la naturaleza y sus fenómenos. Muchas veces se encuentran flores y plantas con proporciones de oro. Entre los animales también hay ejemplos: la estrella de la mar, la concha del fósil animado Nautilus (5. irud. ). El átomo de carbono, es decir, los diamantes y el compuesto básico de los seres vivos, tiene también una estructura de oro.