Zientziaren sorrera Grezian: eskola pitagorikoa

Eskola joniarraren joera nagusia arrazionalista bazen ere, eskola pitagorikoek hartzen zuena orfismotik eratorritako joera mistikoa izan zen eta hau behaketa eta ikerketara bultzatua zegoen.

Pitagora (K.a 582-500) Samos-en jaio zen, baina 530. urte inguruan Hego Italiara joan zen.

Eskola honetakoak Unibertsoaren sortzailea den adimen-printzipio baten bila aritu ziren. Substantziaren trasformazioan oinarritzen zen eskola joniarraren joera alde batera utzirik, mundu materialaren oinarrian, adimenak eskura dezakeen gauza bakarra zenbakia dela ezarri zuen eskola honek.

Nahiz eta eskola hau sortu baino lehen, babiloniarrek ortze-gorputzei zenbaki-proportzio xeheak egokitu bazizkieten eta Anaximadrok berak izar, Ilargi eta Eguzkiarekiko distantziak r-diskoaren lodiera bederatzi, hamazortzi eta hogei aldiz handiagoa gela esan bazuen ere, Naturaren alderdi guztietara zenbakiak egokitzea eskola pitagorikoaren emaitza da.

Afrodita.

Gu zenbakien ideia (hots, kantitate abstraktuak) erabiltzera ohituta gaude. Ez daukagu inongo arazorik bost edo ehun zifrez, zer diren alde batera utzita, lan egin ahal izateko. Horregatik, filosofiarentzat nahiz matematikarentzat gauza heterogenoen taldetan bostaren edo ehunaren kontzeptuen amankomuntasuna aurkitzeak eta isolatzeak suposatzen duen zailtasunaz ohartzea, benetan gaitza da guretzat.

Matematikaren arloan, aritmetika sorterazi zuen honek. Filosofian berriz mundu erreala ren oinarrian zenbakia aurkitzen denaren ideia. Aristotelek zera zioen: "Dirudienez, zenbakia oinarria da, hots, gauza errealak osatzen dituen materia, pitagorakoen ustetan". Pitagorakoek musikaz ere lan egin zuten eta arlo honetan oinarri-nota baten bostuna eta zortziduna ematerakoan, soka baten luzerako 6/4/3 erlazio finkoetan aurkitzen zirela ikusi zuten. Oinarrizko entitateak unitate definitu eta zatiezinez osatuta zeudenaren ideiak, laguntza ederra jaso zuen horretatik.

Orduan, zenbaki erlatiboen eskema honetan funtsatuta, Unibertsoaren teoria osoa eraiki nahi izan zuten. Zenbaki erlatibo hauek, espazioko unitate zatiezi hei zegozkien. Beren ustez, planeten eta Lurraren arteko distantziek progresio musikal bati jarraitu behar zioten. Honek "esferen musika" sorteraziko luke.

Aurreneko lau zenbakien batura izanik, hamarra zenbaki perfektua zen; horregatik, urtzeko gorputzek ere hamar izan beharko zuten. Baina, bederatzi baino ikusten ez zutenez gero, "kontralur" ezinikusi baten hipotesia plazaratu zuten. Aristotelek, kritikatu ondoren, ekintzen bidez suntsitu zuen amets hau.

Hala ere pitagorikoek kosmogonia aurrera eraman zuten. Honi buruz dakigun gehiena Kro tonako Filolaoren bidez dakigu. Hau K.a V. mendearen erdi aldera bizi zen. Nonbaiten, Lurra esferikoa zenaz ohartu ziren eta itxurazko zeruen errotazioa errazago adierazten zen, baldin Lurraren errotazioa onartzen bazen. Lurraren biraketa hau ez litzateke bere ardatzaren inguruan izango; espazioko puntu finko baten inguruan baizik, eta diametroaren beste muturrean kontralurrak biratuko luke.

"Jainkosa bikiei titia emanez" K.a. VI. mendeko eskultura.

Dena dela, errotazio honetan Lur-esferaren bizia duen erdia beti kanpoko urtzearen aldean dagoenez gero ez dago esandako kotralurra ikusterik. Ikusten ez den puntu finkoan su handi bat piztuta egongo litzateke: "unibertsoko aldarea", hain zuzen. Ideia honek eritu oker bat sorterazi zuen, hau da, Aristarkok eta Kopernikok baino lehenago pitagorikoek teoria heliozentrikoa ezarri zutenaren eritua alegia.

Kosmogonia aldetik Pitagorak eta bere ikasleek elementu material bakarraren ideia alboratu zuten, materia lur, ur, su eta airez osatuta dagoela onartzeko. Elementu hauek, lau kualitateren binakako konbinazioz osatzen zirela pentsatzen zuten: beroa, hotza, hezetasuna eta lehortasuna. Honela, ura, adibidez, hotza eta hezea den bitartean, sua beroa eta lehorra da.

Lehen pitagoratarrek, geometria aritmetikarekin uztartzen zuten. Pitagorak eman zuen irakaskuntza; abstrakzioan, definizio zehatzetan eta demostraziotan oinarritzen zen. Egyptoko eta Mesopotamiako ezaguera praktikoak kontutan hartzen baditugu, lerro, puntu, etab. ideia abstraktuak noiz eta non agertu ziren jakitea zaila da; hala ere, lorpen hauek ohituraz pitagoratarrei eransten zaizkie eta hauekin batera geometria abstraktuaren sorrera. Eskola honek, besteak beste, triangelu baten angeluek bi angelu zuzen osatzen dutela edo n aldean ko poligono baten barneko angeluek (2n 4) angelu zuzen balio dutela demostratu zuen.

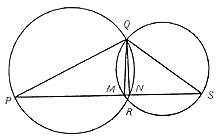
Eskola honen fundatzailearen lorpenik ezagunena "Pitagoraren teorema" izenez bataiatua izan den teorema da: "Triangelu zuzen baten hipotenusaz eraikitako karratua, triangelu horren beste bi aldez eraikitako karratuen ba tura adina da" (Euklide, "Elementuak", I, 47).

BCDE = a hipotenusaz eraikitako karratua.
AFGB = c aldeaz eraikitako karratua.
BHJI = b aldeaz eraikitako karratua.
AFGB + BHJI = BCDE-(BGE + KDE) + (ABC + CFK + BLJI).
Baina, ABC = BGE, biak triangelu zuzenak eta aldeak berdinak dira.
BLJI = FKMD, simetriaz. Beraz:
CFK + BLJI = CFK + FKMD = CMD
Baina, CMD = KDE, biak triangelu zuzenak dira eta aldeak berdinak.
Beraz:-(BGE + KDE) + (ABC + CFK + BLJI) = 0
Eta AFGB + BHJI = BCDE

Plutarkok, Diogene Laertziok eta Proklok diotenez Pitagorak enuntziatu zuen teorema hau, eta bere sortaldeko jatorria alde batera utzita (dirudienez babiloniarrek ezagutzen bait zuten) matematikaren historian oinarri sakonenetako bat da.

Eskola honetan zenbakien doktrinan dagoen Naturaren ideia mistikoak, pitagoratarren ustetan aurkako elementuek zuekaten garrantzia frogatzen du: argia eta iluntasuna, maitasuna eta gorrotoa, etab. Ideia mistiko hau berriro Alkmeon sendagilearengan agertu zen berriro.

Honen erituz, gizona mikrokosmo bat da, hau da, Unibertso txiki bat: gorputzak munduaren egitura isladatzen duen bitartean, arima zenbakiaren armonia da.

Joniatarrek materiaren filosofia defendatzen bazuten, pitagoratarrek itxuraren filosofiaren alde burruka egiten zuten. K.a. V. mendean azkeneko eskola hau bi adarretan banatu zen: bata erlijio-erakunde bihurtu zen eta besteak ia zientifikoa zen zenbakiaren teoria bat garatu zuen.