A creación da ciencia en Grecia: una escola pitagórica
1986/04/01 Bandres Unanue, Luis Iturria: Elhuyar aldizkaria

Aínda que a tendencia dominante da escola jónica era a racionalista, o que tomaban as escolas pitagóricas foi una tendencia mística derivada do orfismo, que se centraba na observación e a investigación.
Pitago (582-500 a.C.) naceu en Samos, pero cara ao ano 530 foi a Italia do Sur.
Os desta escola buscaron un principio de intelixencia que é o creador do Universo. Á marxe da tendencia da escola jónica baseada na trasformación da sustancia, esta escola estableceu que, na base do mundo material, o único que a mente pode adquirir é o número.
A pesar de que antes da creación desta escola, os babilonios adaptaron aos corpos de amasado minuciosas proporcións numéricas e o propio Anaximadro falou de sálgaa nove, dezaoito e vinte veces o grosor do disco r, nove, dezaoito e vinte veces maior, a adaptación dos números a todos os aspectos da Natureza é o resultado dunha escola pitagórica.

Nós estamos afeitos utilizar a idea de números (é dicir, cantidades abstractas). Non temos ningún problema en cinco ou cen cifras, independentemente do que son, paira poder traballar. Por iso é polo que, tanto paira a filosofía como paira as matemáticas, sexamos conscientes da dificultade que supón atopar e illar a unidade dos conceptos do cinco ou do tecido en grupos de cousas heteroxéneas, sexa realmente difícil.
No campo das matemáticas, isto xerou aritmética. A idea de que en filosofía se atopa o número na base do mundo real. Aristóteles dicía: "Parece que o número é a base, é dicir, a materia que forma cousas reais, en opinión dos pitagóricos". Os de Pitágoro tamén traballaron en música e viron que ao dar o quinteto e oitava dunha nota base neste campo atopábanse nunhas relacións fixas de 6/4/3 de lonxitude dunha corda. A idea de que as entidades básicas estaban formadas por unidades definidas e indivisibles, recibiu diso una gran axuda.
Entón, baseándose neste esquema de números relativos, quixeron construír toda a teoría do Universo. Estes números relativos correspondían a esas unidades espaciais indivisibles. Consideran que as distancias entre os planetas e a Terra debían seguir una progresión musical. Isto crearía a "música das esferas".
Sendo a suma do catro primeiros números, a décima era un número perfecto, polo que os corpos de fusión debían ter tamén dez. Pero como só vían nove, lanzaron a hipótese dun imprevisto "contralur". Aristóteles criticou este soño con accións.
Con todo, os pitagóricos levaron a cabo a cosmogonía. A maior parte do que sabemos respecto diso sabémolo a través do Filolao da tonelada Kro. Vivía a mediados do século V a.C. Nalgún lugar, déronse conta de que a Terra era esférica e a rotación dos ceos aparentes era máis fácil de expresar se se aceptaba a rotación da Terra. Este xiro da Terra non se produciría sobre o seu eixo senón sobre un punto fixo do espazo, virando a contralura no outro extremo do diámetro.

Con todo, como nesta rotación a metade que ten a vida da Esfera Terrestre está sempre no lado da fusión exterior, non é posible ver a mencionada crista. No punto fixo que non se ve estaría acendido un gran lume: o "altar do universo". Esta idea conduciu á creación dun erito equivocado, do que os pitagóricos estableceron a teoría heliocéntrica antes que Aristarco e Copérnico.
Por parte de Kosmogonia Pitagora e os seus alumnos abandonaron a idea dun único elemento material paira recoñecer que a materia está formada por terra, auga, lume e aire. Estes elementos supuñan una combinación de catro calidades por parellas: calor, frío, humidade e sequedad. Así, mentres a auga é fría e húmida, o lume é quente e seco.
Os primeiros pitágoros combinaban a xeometría coa aritmética. Pitagora impartiu ensino baseado na abstracción, as definicións precisas e as demostracións. Se temos en conta os coñecementos prácticos de Egypo e Mesopotamia, liñas, puntos, etc. é difícil saber cando e onde apareceron as ideas abstractas; con todo, estes logros engádense tradicionalmente aos pitagóricos e con eles a creación da xeometría abstracta. Esta escola demostrou, entre outras cousas, que os ángulos dun triángulo forman dous ángulos rectos ou que no lado n os ángulos interiores dun polígono de c (2n 4) serven de ángulo recto.
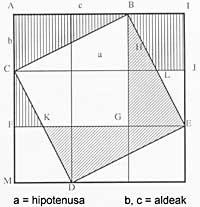
O logro máis coñecido do fundador desta escola é o teorema bautizado como "teorema de Pitagora": "O cadrado construído coa hipotenusa dun triángulo recto é tanto coma se dos cadrados construídos por outras dúas partes dese triángulo" (Euklide, "Elementos", I, 47).
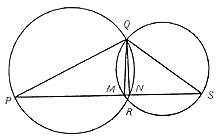
Plutarco, Diogene Laercio e Proklo afirman que este teorema foi enunciado por Pitagora e que, á marxe da súa orixe orixinaria orixinario, ao parecer coñecido polos babilonios, é una das bases máis profundas da historia das matemáticas.
A idea mística da Natureza na doutrina dos números nesta escola demostra a importancia que os pitágoras tiñan dos elementos opostos: a luz e a escuridade, o amor e o odio, etc. Esta idea mística volveu aparecer no médico Alkmeon.
Neste sentido, o home é un microcosmos, é dicir, un pequeno Universo: mentres o corpo reflicte a estrutura do mundo, a alma é a harmonía do número.
Se os jonios defendían a filosofía da materia, os pitágoros desafiaban a filosofía da aparencia. a.C. No século V esta última escola dividiuse en dúas ramas: una converteuse en institución relixiosa e a outra desenvolveu una teoría do número case científico.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia