Historia das cifras (I)

1990/04/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Prehistoria

Os seres humanos de outrora servíanse dos sentidos paira expresar cantidades que, como algúns animais, non eran capaces de distinguir grandes cantidades (como hoxe non entendemos a cantidade de tres trillones).

Os primeiros números que se inventaron foron un e dous. Una paira expresarse (dentro dun grupo). Tamén paira expresar ao pene (paira diferenciarse das mulleres) ou ao home (paira diferenciarse dos animais).

Bia era expresión da duplicidade (empoderamiento e virilidade, vida e morte, verdade e falsa, ben e mal, etc.).

En xeral, pódese dicir que a partir de aí (dous) paira separar maiores cantidades non se utilizaban símbolos especiais e cando tiñan que representar grandes cantidades utilizábase o mesmo símbolo, independentemente da cantidade. As súas testemuñas pódense atopar en varias linguas da súa contorna: no francés son similares trois (tres) e très (moi), no inglés three (tres) e throng (una máquina), no latín só se declinaban o catro primeiros números.

Poderíase dicir, por tanto, que naquela época “a capacidade humana en canto á comprensión dos números non pasaba por catro”. Isto non debe sorprendernos si temos en conta que, a primeira vista, non somos capaces de adiviñar cantos coches hai nunha fila.

Como aprenderon a contar os primeiros habitantes? Paira responder a esta pregunta é necesario distinguir e comprender as dúas formas dos números: cardinal e ordinal. A continuación móstrase un exemplo: Si dicimos “Ten 28 días de febreiro” falamos do número de días de febreiro. Por tanto, o número 28 indica un cardinal. Pola contra, si dicimos “hoxe é 28 de febreiro”, hoxe estamos a dicir que é o día 28 de febreiro. Por tanto, indicamos a orde, é dicir, a forma ordinal.

Nun principio utilizaron o método de emparellamento, é dicir, nun pau que facía una sangría por cada gran, ou collían una pedra, ou tocaban una parte do corpo. Pero iso non foi un gran avance. E é que cando tiñan que volver contar o mesmo tiñan que volver facer sangrías. Por exemplo, cando un rabaño de ovellas saía pola mañá e gardábano pola tarde, tiñan que contar paira saber si perdeuse algunha.

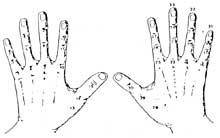
Os papúes de Nova Guinea utilizaban o corpo paira cuantificar a principios deste século. Cada parte do corpo indicaba un número e paira contabilizalo até un número, mantendo a orde no que se tocaban as partes correspondentes a todos os números anteriores. Por exemplo, paira contar 10 tocaban a labra (1) da man dereita, o inquilino (2), o medio (3), o índice (4) e o pulgar (5), daquela a boneca (6), o cóbado (7), o ombreiro (8), a orella (9) e o ollo (10). Pero se una vez feito isto significaban que contaran 10, non tocaban directamente o ollo dereito, senón que comezaban pola labra (1). Isto dinos que non tiñan idea abstracta de números.

O aquí exposto é aplicable aos antigos veciños e sen beizos podemos dicir que o corpo foi o primeiro soporte da aritmética. É o costume de contar cos dedos das mans que aínda perviven.

Poderiamos dicir que con estas técnicas tamén aprenderon a contar ao mesmo tempo que aprenderon a diferenciar ambas as formas. Quedou demostrado que a capacidade de diferenciación era humana. Nós utilizamos ambas as formas tan a miúdo que moitas veces esquecemos a diferenza.

Invención de bases

Una vez conseguida a capacidade de separación, atopáronse con outro problema: pedras, bastóns, muescas, etc., que non podían contabilizar grandes cantidades. uso continuo. A solución non era, por outra banda, dar un nome especial a cada número (número). Por tanto, o ser humano atopouse na necesidade de expresar as maiores cantidades de símbolos como mínimo.

Paira conseguilo, diferentes pobos inventaron diferentes sistemas. O máis estendido é o de base 10. Moitos pobos utilizárono, pero como o fixeron?. Paira dar resposta, imos pór un exemplo (pensa que aínda non sabían escribir): tomaban tiras de diferentes cores; branco, azul, vermello,… Na tira branca de cada animal metían una cuncha. Nesta tira cando había dez cunchas sacábanas e metían una na tira azul. Na tira branca retomábanse as cunchas. Logo, cando na tira azul acumulaban dez cunchas, sacábanas e metían una na tira vermella. Así, cando os animais terminaban tiñan dúas cunchas en tira vermella, seis tiras azuis e tres tiras brancas, indicando o número de 263. Todo isto facíano sen fiar.

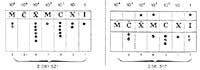
A proba do uso deste sistema podémola atopar en varios idiomas, como o sistema de numeración oral chinés:

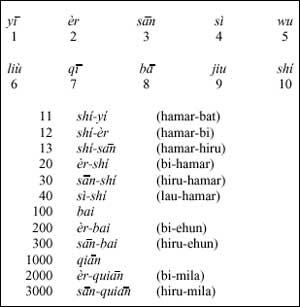
A base 10 ten una vantaxe sobre bases máis grandes, a súa utilidade. Pero, por que non ter bases máis pequenas?. Deberiamos buscar nas declaracións o motivo: 4326 en dúas bases 11100110 Como sabes, necesítanse máis cifras.

Pero o uso da base dez non debe buscarse nas vantaxes matemáticas, senón nas nosas mans. E é que o home sempre utilizou as mans paira contar, e nas mans hai dez dedos.

A base dez non é a única que se utilizou. Tamén se utilizaron as bases cinco, vinte, doce e sesenta.

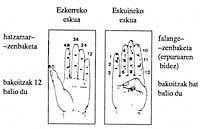
O motivo polo que utilizamos a base 5 atopámolo na man. Paira o cálculo utilizábanse os dedos dunha man e os obxectos agrupábanse en cinco, é dicir, cando na man esquerda había cinco dedos levantados baixábanse e na man dereita levantábase un. Así podían contar até vinte. A pegada de cinco bases pode atoparse en varios idiomas. Por exemplo, na lingua Api das Novas Hebridas

Tamén podemos atopar exemplos de vinte bases sen ir máis lonxe, en euskara. O vinte primeiros números en eúscaro teñen nome e a partir de aí agrúpanse en vinte:

Outros exemplos: Maia, ...

Os pobos que utilizaban esta base tamén tiñan en conta os dedos do pé á hora de contar.

A base doce é máis ampla que a anterior e ten una gran vantaxe sobre dez: O número 12 ten divisores 2, 3, 4 e 6, facilitando o cálculo paira a división. Temos a “ducia” e a “grosa” (12 ducias) que aínda perviven nesta base. Entre os pobos que utilizaron esta base destacan o sumeriano, o babilónico e o romano.

A súa orixe é descoñecido, pero probablemente deberiamos buscalo na man. E é que, eliminando o pulgar, nos outros catro dedos hai tres falanxe, formando un total de doce falanxe. Esta base utilízase actualmente en India, Paquistán, Afghanistán, Egypto, Syria, Turquía, etc.

Sen dúbida, a base máis enigmática é a sexagesimal. Como unidade de contar faise pesado. Con todo, son moitos os pobos que o utilizaron ao longo da historia. Temos as súas pegadas. Por exemplo, a medición do tempo realízase en horas, minutos e segundos; os arcos e ángulos exprésanse en sesenta bases mediante graos, minutos e segundos.

Os sumerianos foron os primeiros en usalo. Estes pasaron aos matemáticos e astrónomos babilonios e estes a os gregos e árabes.

Existen diferentes hipóteses sobre a orixe desta base. Uno deles basea o seu argumento na unión de dúas civilizacións diferentes. Pensemos que se un utilizaba a base dez e o outro a base doce, se recollía ambas, segundo esta hipótese, podían alcanzar a base sesenta. De feito, o múltiplo máis pequeno dos números 10 e 12 é o 60.

Outra posibilidade, na mesma hipótese, estaría composta por cinco e doce bases. A vantaxe deste caso é o produto dos números 60, 5 e 12. Por tanto, non habería que buscar o múltiplo máis pequeno dos comúns. Ademais, na linguaxe sumeriano pódense atopar indicios da aparición de cinco bases:

Primeiras calculadoras

O home, a medida que avanzaba na utilización do concepto de número, trataba de resolver problemas máis profundos. Ao mesmo tempo, os recursos foron mellorando. Podemos dicir que a función máis importante do ser humano de entón foi a de facilitar a contabilidade patrimonial.

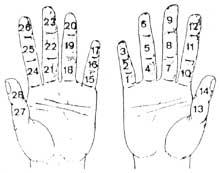
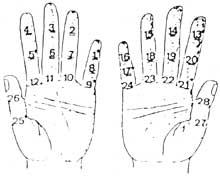
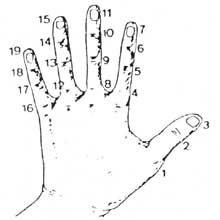
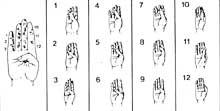
Nun principio contaban coas mans. Por tanto, podemos considerar que a primeira calculadora foi a man. Aínda que non o pareza, coas mans pódense contar dez mil millóns. Desenvolvéronse diferentes métodos utilizando falanxes e articulacións entre falanxes. Paira o seu contabilización, puñan cordóns ou outros sinais nos dedos ou o número que tocaba coa outra man. Pero o uso da man non se limitou a contar. Tamén realizaban cálculos manuais. Por exemplo, sabían multiplicar manualmente.

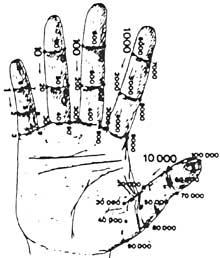
Con todo, coas mans só indicaban os números, pero non podían gardalos na memoria. Cando as relacións entre as sociedades acentuáronse co desenvolvemento do comercio, o home atopouse ante outro problema: como memorizar o que contara até entón?

Dotouse de diferentes métodos e ferramentas paira abordar este problema. A modo de exemplo, mencionaremos o “quipu” (nó) que usaban os cechueros. Tiña una corda principal á que se unían outros grupos de corda, colocados en tramos regulares. Aínda que estas ferramentas cumprían moitas outras funcións, utilizábanse principalmente paira contabilizar. Nas cordas facíanse trabas de números (cantidades). Actualmente este método pódese atopar en: Siberia, Hawai, Nixeria, Novo México, etc.

Outro método prehistórico era o dos ósos ou a madeira. A pegada máis antiga da era “Aurignac” (a. C. Chéganos entre 35.000 e 20.000).

Ao principio o método consistía en facer sangrías. Posteriormente foise mellorando e utilizáronse diferentes sistemas. Cada tipo de obxecto sinalábase cun símbolo especial no pau ou óso. Fai 150 anos levaban os arquivos na Ministra de Facenda do Gran Bretaña. XIX. A principios do século XX os libros de contas no Estado francés, Suíza, Alemaña, etc. eran paus (tayas). Este método utilizouse como recibo, factura ou cartón de crédito nos intercambios entre o comercio e o cliente.

Existe, con todo, outro método que influíu máis na aritmética e contabilidade, é o da acumulación de pedras (pedras, ou bastóns, cunchas, froitos secos, etc.).

A acumulación de pedras, xunto co método da sangría, indica o grao 0 de cálculo, xa que non necesita dun descubrimento abstracto dos números.

Cando o home empezou a utilizar as bases, resultou bastante flexible paira avanzar.

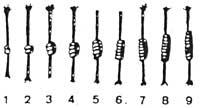
Na actualidade utilízase o método da conxestión nalgúns tributos como signo de diferenciación e riqueza. Este método axudou ao home a formarse no cálculo. A palabra cálculo provén da palabra latina “calculus”, cuxo significado é “pedra redondeada”. A mesma etimología pódese atopar noutras linguas: en grego a palabra “pséphos” ten significados “números” e “una pedra”; en árabe as palabras “haswa” (arrecife) e “ihsa” (numeración, estatística) teñen a mesma raíz. Os birlos son a orixe dos marcadores de ábaco e bólas.

Os primeiros ábacos facíanse no chan mediante gabias paralelas. Posteriormente en taboleiros ou pedras, mediante liñas paralelas. Cada gabia e liña tiña un valor diferente, estando o valor suxeito á base. As pedras, os calculus, e máis tarde as fichas, colocábanse sobre gabias e raias, cada una delas tomaba o valor da liña ou gabia.

No lado Este, pola contra, creáronse marcadores de bólas co mesmo funcionamento. Ademais de contar con estes instrumentos, tamén podían realizar operacións. Na actualidade aínda existe una gran costume de utilizar os ábacos en China, Xapón, URSS e todo o leste.