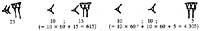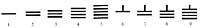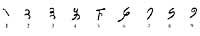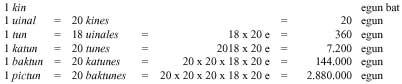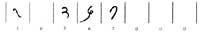Història de les xifres (IV)

1990/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

En els sistemes de numeració que hem vist fins ara les xifres tenien un valor fix. En el sistema xinès s'escrivia el símbol de l'ordre entre els valors de diferent ordre.

Pas decisiu

En els sistemes de numeració que hem vist fins ara les xifres tenien un valor fix. La xifra romana L, per exemple, en qualsevol lloc, costarà sempre 50. En el nostre sistema no: En el 79876 el primer set de l'esquerra presa el valor 70.000 i l'altre el valor 70, és a dir, el valor d'una xifra depèn de la posició. A això se'l denomina principi de posició.

Sistema

xinès

entre valors de diferent ordre

s'escrivia el símbol de l'ordre.

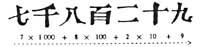
Fins a aconseguir aquest principi l'home va donar moltes voltes a les xifres.

Aquesta regla bàsica va ser inventada pels babilonis. A principis de l'any 2000. En l'època del rei Hamurabi (a. C. 1792-1750) va ser un dels primers astrònoms i matemàtics babilònics a crear un sistema de numeració. El valor de la xifra variava segons la posició. Escrivien els números en la base sexagesimal mitjançant dos símbols

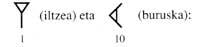
Números de l'1 al 59 per principi additiu i a partir d'aquí per principi de posició. A pesar que aquest sistema era similar al nostre, en cada ordre d'unitats utilitzava el principi additiu i no utilitzaven símbols diferents per a representar números fins a 59. Això va suscitar molts dubtes. Però aquesta dificultat oculta altra més profunda

té. Com indicar que no es necessiten xifres en un ordre d'unitats? És a dir, com escriure els números 203, 1003? Si es vol utilitzar el principi de posició, s'ha d'escriure en 3 en primer lloc, 2 en el tercer i 2 en el segon. Els babilonis encara no coneixien aquest concepte. 1200 anys.

Al principi deixaven un buit entre dues ordres

Però això no va ser una solució adequada. Finalment, a. C. III. En el segle XX es va inventar un altre símbol per a expressar l'absència d'ordre

Aquest és el zero més antic. Però això no ho van prendre com un número, sinó en el sentit del buit.

Dos mil anys després els xinesos van erigir aquesta regla. Allí durant la dinastia (a. C.) II - d. C. III. segles) van inventar un sistema de ratlles horitzontals i verticals.

La línia horitzontal es valorava en 5. A partir d'aquí els números es representaven segons el principi de posició:

Aquest sistema va tenir un problema: quan les xifres d'un número s'escrivien només amb línies verticals (434), no es podia saber quin número era (344, 443, 2324, ...). Més tard van intercanviar línies horitzontals i verticals entre si, i més tard es van barrejar aquests dos sistemes, representant ordres successives amb diferents sistemes: unitats, percentatges, deu mil, ... escrivint amb línies verticals i uns altres, deu, mil, ... amb línies horitzontals. Es van solucionar alguns problemes. No obstant això, per a comprendre el concepte zero va haver-hi segles d'existència.

Per a expressar la falta d'un ordre, alguns deixaven un buit. Això no va ser un bon camí i finalment es va valer del símbol de la tradicional numeració xinesa. Uns altres van anotar els números dins d'uns quadres, deixant la casella de l'ordre que faltava. Però C. III. Fins al segle XX no van aconseguir el zero. Es va aconseguir gràcies a la influència de matemàtics i astrònoms hindús.

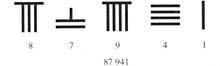
Segles després, a Centreamèrica els maies van aconseguir els mateixos avanços. En el primer mil·lenni de l'era cristiana van aconseguir el cim de la seva societat en molts camps: art, escultura, arquitectura, matemàtiques, educació, ... En astronomia, per exemple, van obtenir dades més precises que els europeus; en matemàtiques també coneixien el principi de posició i el zero.

Codex de Dresden (IX. En el segle XX, els maies sazerdote tenien encara un sistema de base vint (amb zero i amb principi de posició).

Segons aquest sistema, els dinou primers números s'escrivien en punts i ratlles. A partir d'aquí els números es representaven per columnes. En les columnes hi havia tantes plantes com ordre. Unitats per a números de dos ordres en l'inferior i de vint en el superior. Tres

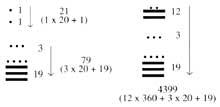
en les d'ordre, en la tercera planta no s'escrivien els quatre percentatges, sinó els de 360. En les següents plantes es va seguir la base de vint. Per això, les de la 4a planta són múltiples de 7.200, les de la 5a són múltiples de 144.000, ... Perquè les xifres guardin el seu lloc quan faltava un ordre, van inventar el zero.

Al principi, juntament amb les xifres, escrivien els símbols de la seva ordre. Més tard es van adonar que aquests símbols no eren necessaris i els van retirar. La raó de l'ordre 360 de la tercera planta cal buscar-la en astronomia. En els calendaris maies la primera planta indica els dies, la segona els mesos (20 dies), la tercera els anys (360 dies), ...

Aquests són els primers pobles que van crear la xifra zero i el principi de posició. No obstant això, no van saber treure profit. Durant els dos mil anys que van utilitzar el sistema als babilonis no se'ls va ocórrer associar cada xifra a un signe especial; els xinesos van continuar utilitzant l'escriptura ideogràfica i els maies escrivien els números amb un principi additiu.

Gràcies al zero, els babilonis van aconseguir notables avanços, ja que l'utilitzaven com a agent aritmètic. Els maies, per la seva singularitat en la tercera planta, no van poder aplicar els avanços en les operacions. Gràcies a aquestes deficiències, aquests sistemes no van servir per a operar.

Sistema de numeració modern

Estem prop del sistema de numeració modern. Qui té l'honor de ser inventor del nostre sistema?

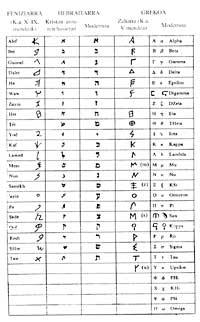
A principis d'aquest segle alguns historiadors van donar aquest honor als grecs. Però no hi ha cap document que el demostri. Com hem vist abans, els grecs van utilitzar al llarg de la història dos sistemes: un equivalent al sistema romà i un altre alfabètic. En cap dels dos casos la xifra era zero. Fins i tot desconeixien el principi de posició.

Llavis

sense els matemàtics hindús mereixen l'honor. Nord de l'Índia. L'avantpassat del nostre sistema va néixer cap al segle V.

L'antiga numeració hindú semblava a les que hem vist, però tenia ja una característica del sistema modern: les nou xifres es representaven amb diferents símbols. No obstant això, per a escriure un número utilitzaven el principi additiu. Per tant, van trobar límits similars. Com no podien escriure números grans, se'ls va ocórrer escriure amb totes les lletres:

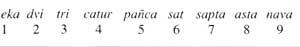
Els nou primers números tenien un nom especial. Van posar noms especials a Hamarra i les seves verdures. Els altres números s'escrivien amb noms composts. Ells utilitzaven un ordre creixent d'esquerra a dreta. Entre les unitats i decimals per a escriure un número s'intercalava el nom de deu, entre deu i cent el nom del teixit, etc.

A causa del costum i per necessitat breu, matemàtics i astrònoms hindús van eliminar els noms de la base i les seves verdures, mantenint l'ordre. D'aquesta manera van obtenir una numeració de posició verbal. Aquest avanç va suposar un altre: es van adonar que necessitaven alguna cosa per a expressar la falta d'un ordre. Per a això es va utilitzar la paraula sunya (buit). Ara sí que tenien els tres pilars del sistema modern:

• diferents xifres per a números de l'1 al 9
• principi de posició
• zero

No obstant això, havien de superar un obstacle. El seu nou sistema, inclòs el zero, era verbal. Les dues últimes bases, segons els documents coneguts, a tot tardar en C. Ja sabien en el segle V. El 25 d'agost de 458 del Calendari Julià, publicat pels membres del moviment religiós hindú diví en el tractat anomenat Lokavibbar, apareix el número 14236713:

triny ekam sapta sat trini dve catvary ekakam

(literalment tres set sis tres quatre)

És de destacar que al costat de cada enunciat apareix la paraula sthanakramad (literalment: en ordre de posició) com a ajuda per a no experts. Un altre esment especial: per a no avorrir-se de la repetició d'una xifra en un número van utilitzar els sinònims del nom d'aquesta xifra:

Això poetizó les matemàtiques i va facilitar la memorització del càlcul.

Sabem que els aritmètics hindús eren molt hàbils en el càlcul. Però abans d'aplicar la base del nostre càlcul (com en altres països) es van utilitzar diferents eines (àbac, taula de comptatge, ...). Els hindús representaven l'àbac de columna en la sorra. En la primera columna de la dreta les unitats, en la segona les desenes, en la tercera els percentatges, etc. utilitzant les xifres antigues que escrivien. Però aquest mètode era molest i difícil.

d. C. VI. A principis del segle XX es van barrejar les numeracions oral i escrita, en imposar-se a l'altra els avantatges de la numeració oral. Al mateix temps, seguint la imatge de l'àbac, van canviar el sentit de l'escriptura dels números. El zero es va expressar amb un punt o amb un petit cercle per motius desconeguts. A poc a poc es van anar introduint canvis importants. A més es van escurçar i van millorar les regles. Gràcies a la seva tenacitat, els hindús van aconseguir fa quinze segles una tècnica d'operació tan senzilla i ràpida com l'actual.

No obstant això, havien de fer l'últim pas: la normalització del concepte abstracte zero, ja que fins llavors el buit, la columna, o l'espai buit, tenia significat. Com tots els zeros anteriors s'utilitzava per a emplenar buits. Però els hindús van ser capaços de superar aquesta barrera i, a mitjan segle, el zero tenia significat buit i res.

Gràcies a això, en un treball datat l'any 628, el matemàtic i astrònom Brahmagupta va demostrar com les sis operacions bàsiques (suma, resta, multiplicació, divisió, potències i arrels) podien realitzar-se amb el patrimoni, el deute i el no-res (és a dir, amb números positius, negatius i nuls). Va néixer l'algebra modern.